什么是反向传播算法

本文翻译自：http://colah.github.io/posts/2015-08-Backprop/

背景介绍

反向传播算法在现在神经网络中是一个非常关键的算法，它使得训练深层模型成为可能。相比直观幼稚的实现，它的训练速度可以快到几千万倍，好比一个模型一周训练时间跟200,000的训练时间

不仅在深度学习领域，反向传播算法在很多领域中，比如气象预报和数值稳定性分析，都是非常重要和有力的计算工具。事实上，在其他领域反向传播算法有很多的体现，仅仅是叫法不一样而已。不考虑应用领域，方向传播算法有一个通用的名称叫做“方向微分”。

本质上，方向传播算法是快速计算微分的方法，不仅在深度学习领域，在任何数值计算场景，都是应该掌握的工具。

计算图

计算图是一种很好的可视化数学表达式的方法。让我们来看一个例子，$e = (a+b) * (b+1)$，这里面有个三个数学运算：两个加法和一个减法。为了方便我们讨论，我们引入 另外两个中间变量，$c$ 和 $d$，我们可以得到如下三组表达式：

$$ c= a+b \ d=b+1 \ e=c*d $$

每一个表达式左边的二元运算符的左右两个操作数，可以看做输出节点的输入，输出节点为二元运算符的运算结果。在输入节点和输出节点之间画一条有向线段以表示其之间的关系。因此，上例的计算图可以表示为：

这样的图在计算机科学中非常普及，尤其是在函数式编程实践中。你会发现，诸如调用图，依赖图都与计算图非常相似。它们也是目前非常流行的深度学习框架 [Theano](http://deeplearning.net/software/theano/) 的核心抽象。

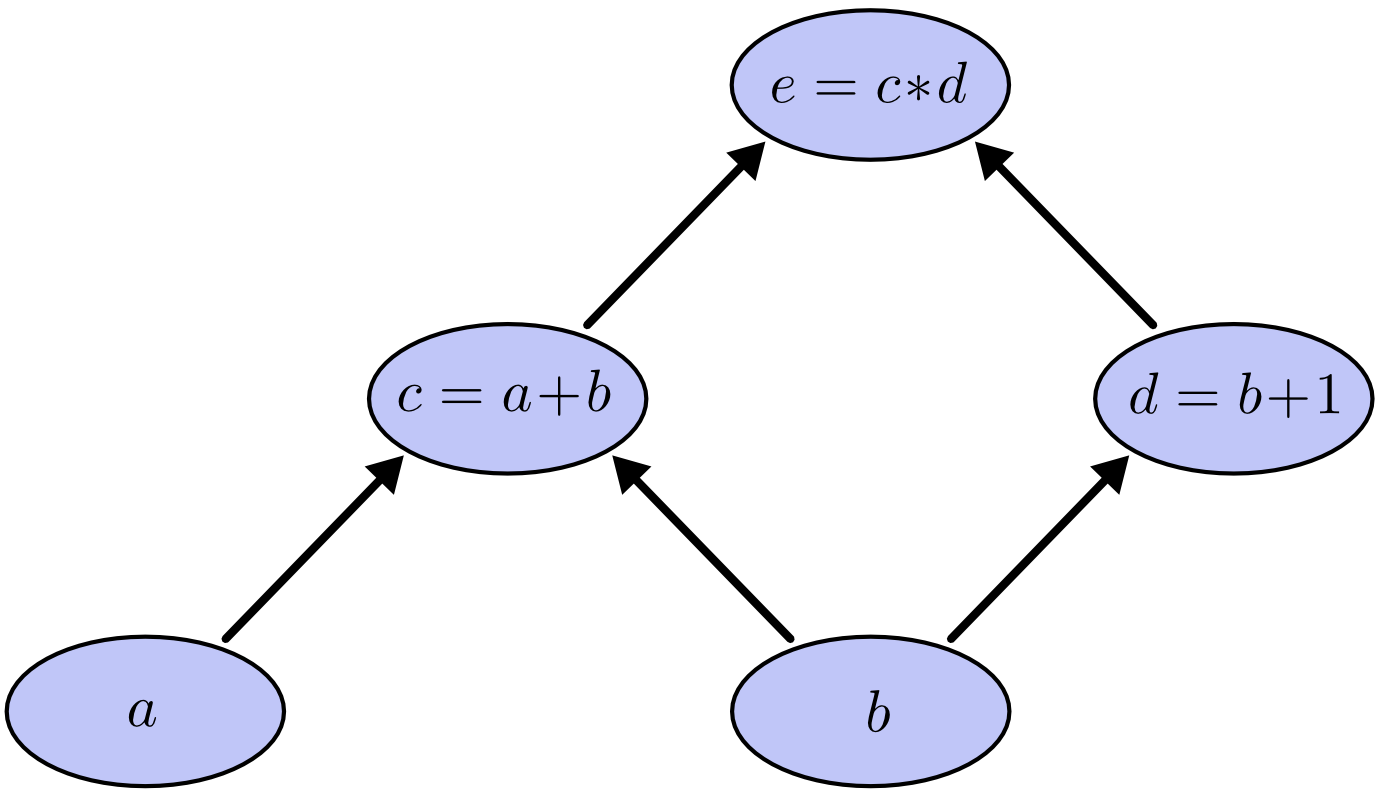
通过给输入节点赋值，我们可以对计算图求值，如果我们给定 $a=2$ 和 $ b=1$，我们可以得出 $c=6$。

计算图上的求导

要理解计算图上的求导，最关键的是理解偏导数，如果 $a$ 直接影响 $c$， 我们想知道如果改变一点点$a$会如何影响$c$，我们称之为$c$对$a$的偏导数。 要对偏导数求值，我们需要了解偏导数的加法和乘法定理：

$$ \frac{\partial(a+b)}{\partial a} = \frac{\partial a}{\partial a}+ \frac{\partial b}{\partial a} = 1 \
\frac{\partial(uv)}{\partial u} = u \frac{\partial v}{\partial u}+ v\frac{\partial u}{\partial u} = v $$

下面的图标出了每条边对应的偏导数：

如果我们想要知道两个没有直接相连的节点是如何互相影响的呢？让我们来看 $e$ 是怎么被 $a$ 影响的。 如果我们以速度为 1 改变$a$，$c$就会以速度为1改变。相应地， $c$以速度为 1 改变导致 $e$ 以速度 2 改变，所以 $e$ 相对于 $a$ 改变的速率是 $1 * 2$。

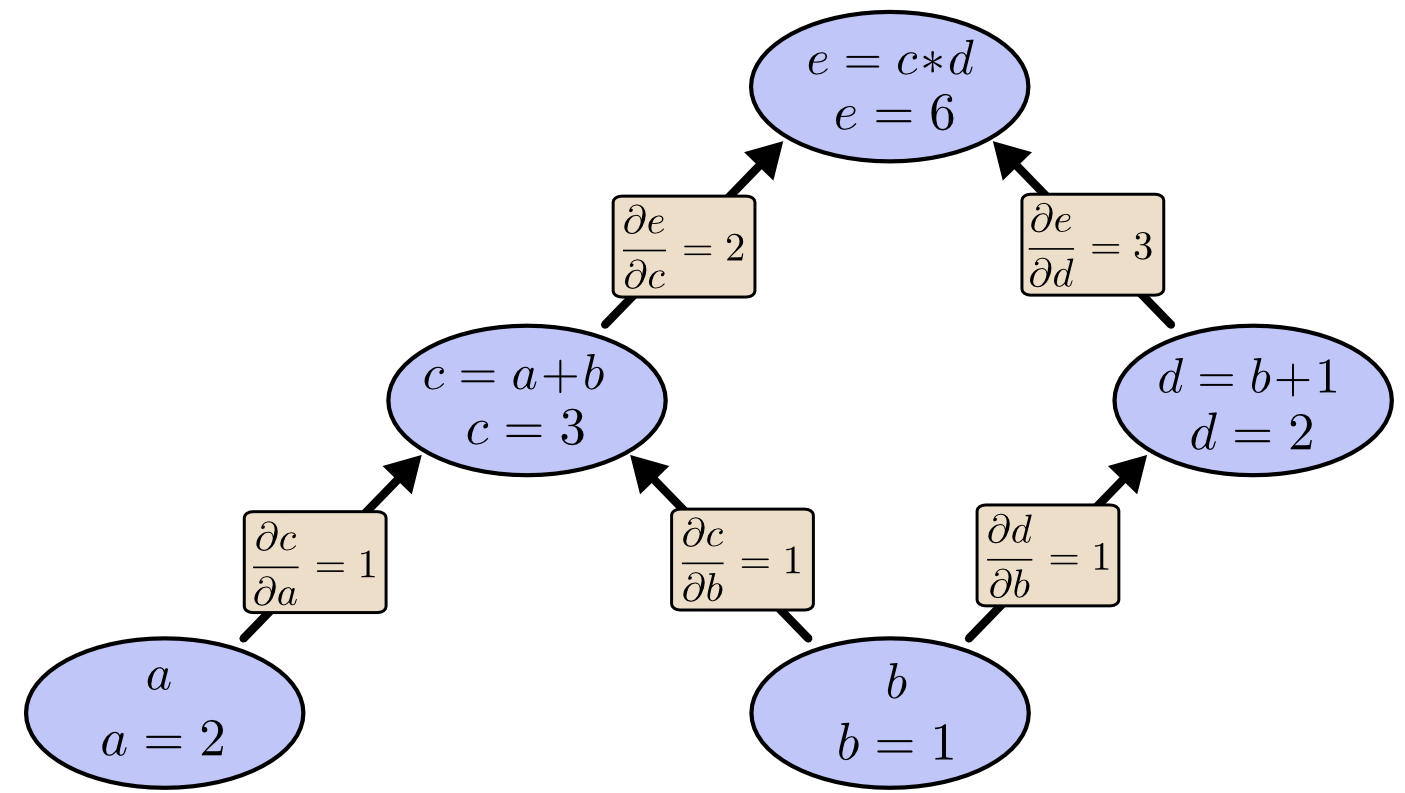
大致的规则是这样的：分别对从影响因子节点到被影响节点的所有边上的偏导数做乘法，然后将乘法结果相加。 举个例子，为了得到 $e$ 相对于 $b$ 的偏导数我们有：

$$\frac{\partial e}{\partial b} = 12 + 13 $$

这个式子解释了 $e$ 是如何通过 $c$和$d$ 影响 $e$的。这种“路径加法”法则可以当做是一种多变量链式法则。

路径分解

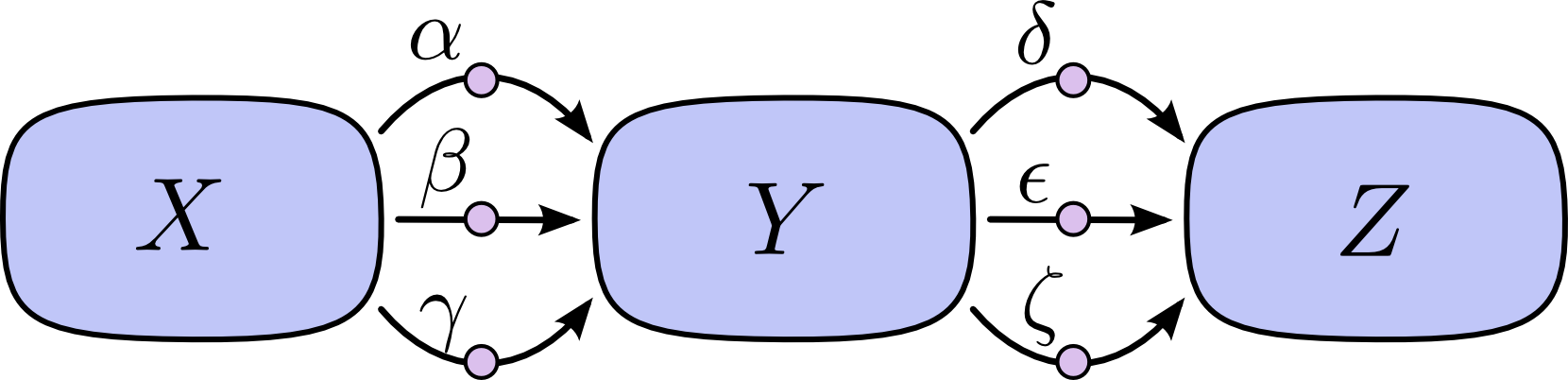
“路径加法” 问题会引来组合爆炸，在下面图中， $X$ 到 $Y$以及 $Y$ 到 $Z$ 中分别有3条路径，如果我们通过“路径加法”法则求 $\frac{\partial Z}{\partial X}$，我们需要计算 9 条路径：

$$\frac{\partial Z}{\partial X} = \alpha\delta + \alpha\epsilon + \alpha\zeta + \beta\delta + \beta\epsilon + \beta\zeta + \gamma\delta + \gamma\epsilon + \gamma\zeta $$

这个例子中仅仅只有 9 条路径，在很多应用中路径会多得多，所以这种方法计算会导致复杂度成指数级增长。

考虑乘法的结合律，上式可以写成：

$$\frac{\partial Z}{\partial X} = (\alpha + \beta + \gamma)(\delta + \epsilon + \zeta) $$

这两个式子正好引入了“前向微分”和“方向微分”， 后者比前者在计算上更加地效率，而且结果完全一致。

前向微分模式从输入开始到最终节点停止，在每个节点上将所有指向该节点的边相加，每一条边代表着对该节点的影响。通过将这些相加起来，我们最终可以得到相对于输入的导数。

然而，在使用这种方法计算时你可能不需要计算图，你会发现前向微分发是微积分入门课上你隐式学习到的方法。

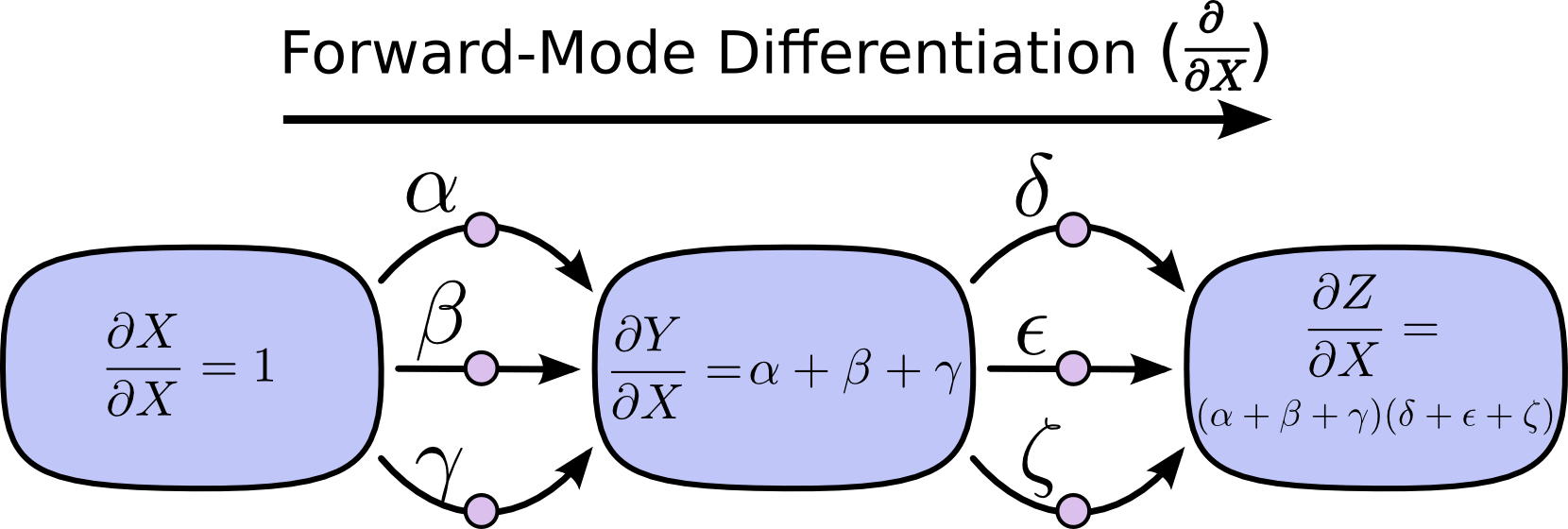
反向微分模式从计算图的输出开始向输入节点移动，在每一个节点，融合所有散出的路径。

前向微分模式追踪了某个输入对每个节点的影响，然而，反向模式记录了每个节点如何影响输出的。可以说，前向模式对每个节点计算$\frac{\partial}{\partial X}$， 方向模式对每个节点计算 $\frac{\partial Z}{\partial}$ 。

计算的好处

至此， 你可能要问问什么大家都关心反向微分，它看起来像是做同一件事情的另一种奇怪的方法，它有什么优点呢？

让我们来看我们之前的例子：

我们可以使用前向微分模式从 $b$ 往上， 这个可以求出每个节点相对于 $b$ 的导数。

我们计算了 $\frac{\partial e}{\partial b} $, 这是输出关于其中一个输入的微分。

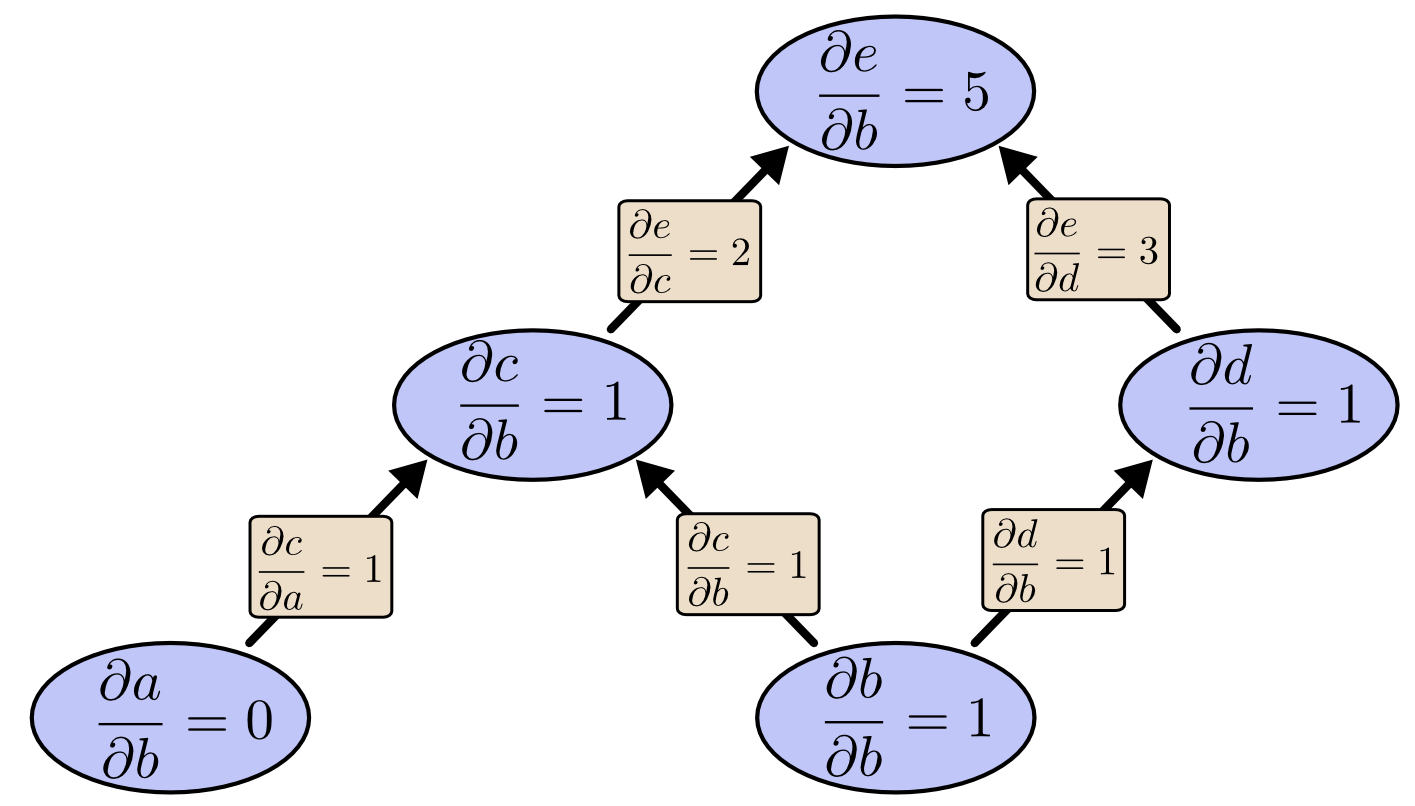
如果我们从 $e$ 开始计算方向微分呢？这将会得到 $e$ 相对于每个节点的导数。

当我之前说方向模式微分可以得到 $e$ 相对于每个节点的导数， 我是指真的是每一个节点。我们可以得到 $\frac{\partial e}{\partial a}$和 $\frac{\partial e}{\partial b}$， 这是 $e$ 关于两个输入的导数。前向微分模式计算的是输出相对于一个输入的导数，而反向模式计算的是输出相对于所有输入的导数。

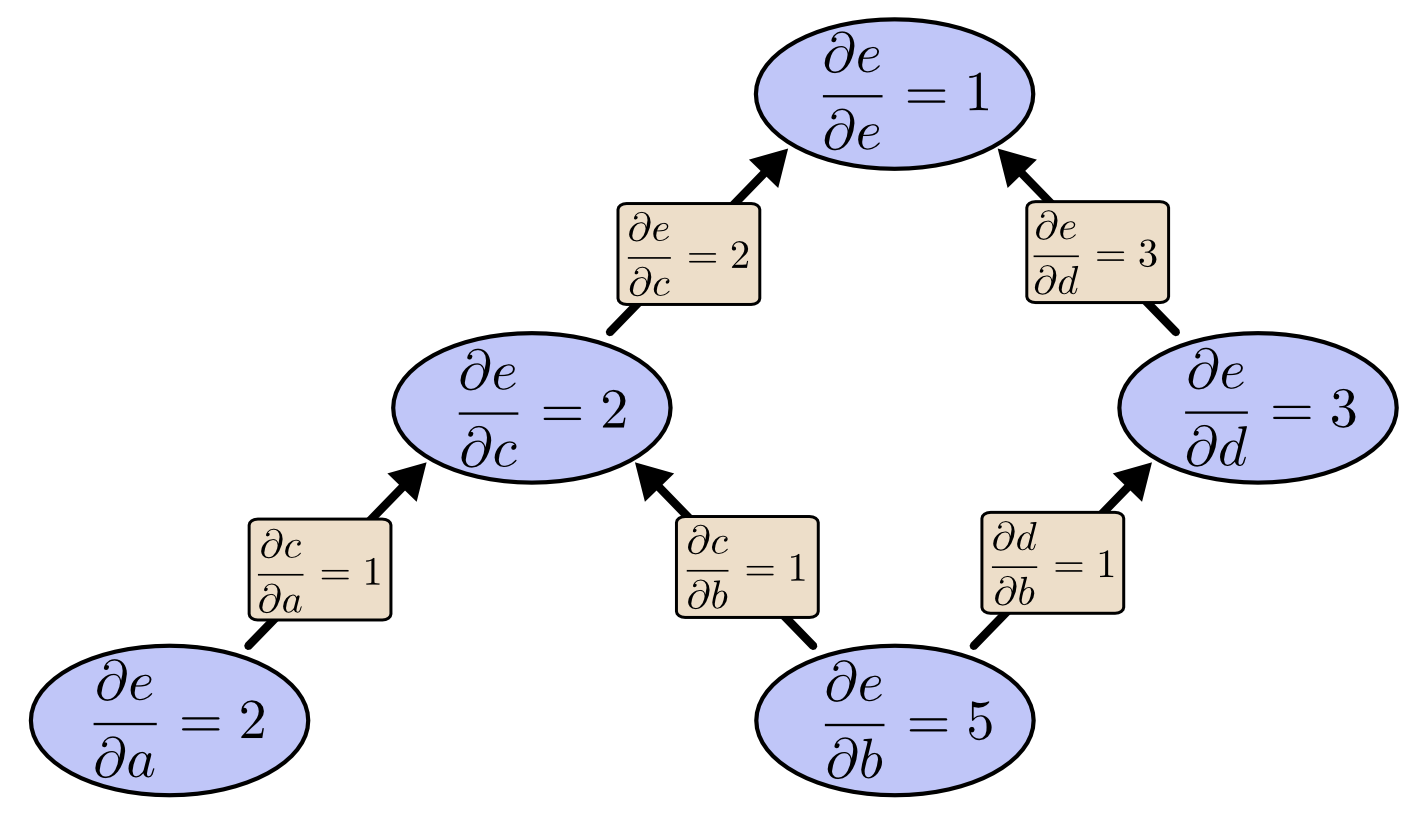
对于这张图，输出只被两个因素影响，但是考虑100万个输入和一个输出呢。前向模式需要循环100万次来计算100万个导数。但是反向模式只需要一次。

当训练神经网络的时候， 我们认为损失（用于表示神经网络性能的好坏）是网络参数的函数（用于描述网络的行为）。为了得到收敛的参数，我们需要使用梯度下降，要计算梯度就必须计算损失函数对于所有参数的导数。经常我们会遇到有成千上万， 甚至千万参数的情况。所以，反向模式微分，也被称为反向传播在深度学习参数学习中可以大幅度地提高性能。

（有没有什么情况前向微分模式更好的情况呢？答案是肯定的。我们知道反向模式微分可以给我们一个输出相对所有输入的导数， 前向模式微分可以给我所有输出相对于一个输入的导数。如果我们有一个函数拥有非常多的输出，那么前向微分模式将变得非常非常非常地快。）

这个东西难么？

当我理解了反向传播算法时，我的反应是：“哦，这就是链式法则。我怎么今天才发现？” 我并不是第一个拥有这样反应的人。不过，如果你要问“有没有更加智慧的方法能够计算前馈神经网络中的导数呢？” 答案是并不难。

但是我想这应该比想象中要难得多。你会发现，当反向传播被发明的时候， 人们并没有把关注前馈神经网络。同样地，通过求导来训练它也是不为人知的。 只有当你意识到你可以通过快速求导来训练它这个方法才变得显而易见，所以这个事情是个循环依赖。

更糟糕的是， 写出一个环形依赖是很简单的事。通过求导训练神经网络？当然，你很可能被困在局部最小点，而且计算所有导数是相当消耗计算资源的。这些都是因为你知道这个方法可行，才没有在中间就列出一些不去这么干的理由。

这显然是事后诸葛亮。一旦你想出了问题，最困难的部分已经被解决了。

总结

从这篇博客中，你会觉得求导要比想象中的简单。事实上，他们只是没有简单的那么直观而已，我们这些愚蠢的人类还不停地重新发现这个事实。方向传播算法不仅对于深度学习来说非常重要，而且在其他领域里也是真的非常地有用。

还有别的有用的东西么？我想是有的。

方向传播算法很好解释了倒数是如何在模型中流动的。这点对于思考为什么一些模型优化起来非常困难，最经典的例子就是 RNN 的“梯度消失”（Gradient Vanishing）问题。

最后， 我还要说一个从这些技术中学习到广义的算法经验。方向传播算法和前向微分算法（线性化和动态规划））一对比任何你能想到的算法更加有效率的计算导数的方法。 如果你能很好地理解这两方法，你就可以用它们来有效率地计算一些带有导数的表达式。我们会在后面博文中导论。

这篇博文给了读者一个非常抽象的理解，我强烈推荐读者读一读 Michael Nielsen 的文章， 他在那里进行了更加细致的讨论，并且只关注了神经网络。

感谢

感谢 Greg Corrado， Jon Shlens， Samy Bengio 和 Anelia Angelova 对此文的审校。
感谢 Dario Amodei， Michael Nielsen 和 Yoshua Bengio 对解释反向传播算法的讨论。同时感谢那些在座谈会和讲座上解释反向传播算法的人。